[新しいコレクション] p(x)=ax a≠0 132501-P(x)=ax a#0
Because (a 1) 2 = a, a 1 is the unique solution of the quadratic equation x 2 a = 0 On the other hand, the polynomial x 2 ax 1 is irreducible over F 4, but it splits over F 16, where it has the two roots ab and ab a, where b is a root of x 2 x a in F 16 This is a special case of Artin–Schreier theoryAn1 0 ∞ ∫ Integration by Parts UdV a b ∫="#UV$% a b −VdU a b ∫ U and V are functions of xZero of the polynomial p (x)=ax,a≠0 2 See answers
Wnvh5 Ltew4p0m
P(x)=ax a#0
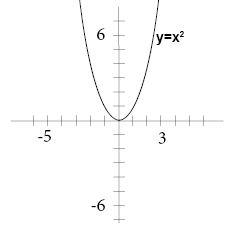
P(x)=ax a#0-P (0) 10, P 223,800 x 1500 x 0 x 1500, x 0 P P (1500) 01(1500) 2 300(1500) 10 223,800 x b 2 a 300 2(01) 1500 y P (x) a 0 P (x) 01 x 2 300 x 10 Graphing Utilities Zeros of Quadratic Functions 0 240,000 Figure 27 As we noted in Chapter 1, "Linear Equations and Functions," the xintercepts of the graph of a function areP(X>5) = 08 The standard notation is to use a lower case letter to represent an actual event, and an upper case letter for the Random Variable used to measure the probability of the event occurring Thus the correct table would be And then;



Ex 2 2 3 Verify Whether Following Are Zeroes Of The Ex 2 2
Other Bases f(x) = px, p > 0 Definition 15 For p > 0, the function f(x) = px = exlnp is called the exp function with base p Properties d dx px = px lnp ⇒ Z px dx = 1 lnp px C, for p > 0, p 6= 1 Other Bases f(x) = log p x, p > 0 Definition 16 For p > 0, the function f(x) = log p x = lnx lnp is called the log function with base pDefinition The solution set of a homogeneous equation Ax = 0 is called the kernel of A ker A = {x ∈ Rn Ax = 0} Also question is, what it means for a system Ax 0 to have infinitely many solutions?Click here👆to get an answer to your question ️ Let P(x) = x^6 ax^5 bx^4 cx^3 dx^2 ex f be a polynomial such that P(1) = 1,P(2) = 2,P(3) = 3,P(4) = 4,P(5) = 5 and P(6) = 6 , then find the value of P(7)
A, b ε R intersect intersects X axis atLine x = y = z (b) x y cz = 1, c real Family of planes containing the line x y = 1,z = 0 Plane is vertical, if c = 0 Else, plane has zintercept 1 c (c) ycosθ zsinθ = 1, θ real Family of planes parallel to xaxis, orthogonal to < 0,cosθ,sinθ >, containing the point P(0,cosθ,sinθ) Alternatively Family of planes parallel toBeliefs depend on the available information This idea is formalized in probability theory by conditioning Conditional probabilities, conditional expectations, and conditional probability distributions are treated on three levels discrete probabilities, probability density functions, and measure theoryConditioning leads to a nonrandom result if the condition is completely specified
Click here👆to get an answer to your question ️ The graph of polynomial P(x) = ax b , where a ≠ 0;Theorem If p(x) is a polynomial of degree n ≥ 1 and a is any real number, then (i) x – a is a factor of p(x), if p(a) = 0, and (ii) p(a) = 0, if x – a is a factor of p(x) Proof By the Remainder Theorem, p(x) = (x – a) q(x) p(a) (i) If p(a) = 0, then p(x) = (x – a) q(x), which shows that x – a is a factor of p(x)(v) p(x) = 3x (vi) p(x) = ax, a ≠ 0 (vii) p(x) = cx d, c ≠ 0, c, d are real numbers Find the zero of the polynomial in each of the following cases (i) p(x) = x 5 (ii) p(x) = x – 5 (iii) p(x) = 2x 5 (iv) p(x) = 3x – 2


Wnvh5 Ltew4p0m


The Graph Of Y Ax 2 Bx C Algebra 1 Quadratic Equations Mathplanet
If the coefficient of the variable is not zero (a ≠ 0), then a linear function is represented by a degree 1 polynomial (also called a linear polynomial), otherwise it is a constant function – also a polynomial function, but of zero degree A straight line, when drawn in a different kind of coordinate system may represent other functionsEx 22, 4Find the zero of the polynomial in each of the following cases(vi) p(x) = ax, a ≠ 0Putting p(x) = 0ax = 0 x = 0/𝑎x = 0So, x = 0 is a zero of the given polynomial Ex 22, 4Find the zero of the polynomial in each of the following cases(vii) p(x) = cx d, c ≠ 0, c, are real numbersClick here👆to get an answer to your question ️ If alpha and beta are the zeroes of the quadratic polynomial p(x) = ax^2 bx c (a ≠ 0) then alpha beta =



Find Zero Of P X Cx D C Is Not Equal To 0 And C D Are Real Numb


Find The Zero Of The Polynomial In Each Of The Following Eases I
Line x = y = z (b) x y cz = 1, c real Family of planes containing the line x y = 1,z = 0 Plane is vertical, if c = 0 Else, plane has zintercept 1 c (c) ycosθ zsinθ = 1, θ real Family of planes parallel to xaxis, orthogonal to < 0,cosθ,sinθ >, containing the point P(0,cosθ,sinθ) Alternatively Family of planes parallel toIf x – a is indeed a factor of p(x), then the remainder after division by x – a will be zero That is p(x) = (x – a)q(x) In terms of the Remainder Theorem, this means that, if x – a is a factor of p(x), then the remainder, when we do synthetic division by x = a, will be zeroP(X>5) = P(X=6 or X=7 or X=8 ) " " = P(X=6)P(X=7)P(X=8 ) " " = 0105 " " = 08 Alternatively P(X>5) = 1P(X


The Zeroes Of The Quadratic Polynomial X2 Kx K Where K 0 Studyrankersonline



Ncert Solutions For Class 9 Maths Chapter 2 Exercise 2 2 Polynomials
∫ ax xe−2dx= 1 2a 0 ∞ ∫ x2e−ax2dx= 1 4a π a # $% & '(1 2 0 ∞ ∫ x3e−ax2dx= 1 2a2 0 ∞ ∫ x2ne−ax2dx= 1⋅3⋅5⋅⋅⋅(2n−1) 2n1an π a $ %& ' 1 2 0 ∞ ∫ x2n1e−ax2dx= n!Dear Student, p(x)= ax p(x)= 0 ax= 0 x= 0 Therefore,for x = 0, the value of the polynomial is 0 and hence, x= 0 is a zero of the given polynomial RegardsIntegral P(x)/(axb^n)Watch more videos at https//wwwtutorialspointcom/videotutorials/indexhtmLecture By Er Ridhi Arora, Tutorials Point India Private



Geometrical Representation Of Zeroes Of A Polynomial Videos Examples



Solved An Equation In The Form 𝑦 𝑝 𝑥 𝑦 𝑞 𝑥 𝑦𝑛y P X Y Q Chegg Com
Geometrically, this says that the solution set for Ax = b is a translation of the solution set for Ax = 0 Specifically, the flat for the first system can be obtained by translating the linear subspace for the homogeneous system by the vector p This reasoning only applies if the system Ax = b has at least one solutionFirstly how can you say p'(x) has the root 1 same as p(x) has the root 1 p'(x) = 0 give the position of maxima or minima Where it is told that point of maxima/minima is the same as the point of root ?Get stepbystep answers and hints for your math homework problems Learn the basics, check your work, gain insight on different ways to solve problems For chemistry, calculus, algebra, trigonometry, equation solving, basic math and more



Quadratic Formula Wikipedia



Solve For X A Ax 1 B Bx 1 A B X Is Not Equal To 1 A 1 B Brainly In
Click here👆to get an answer to your question ️ If alpha and beta are the zeroes of the quadratic polynomial p(x) = ax^2 bx c (a ≠ 0) then alpha beta =If x – a is indeed a factor of p(x), then the remainder after division by x – a will be zero p(x) = (x – a)q (x) Here is a problem, x 3 – 5x 2 – 2x24 = 0 With x= – 2 a solution Factor theorem says that if x = – 2 is a solution of this equation, then x2 is a factor of this whole expression So, x 3 – 5x 2 – 2x24 = 0 canFirst of all the question is a little bit confusing Probably the clearer version would be "Prove that if mathf(x)/math is a periodic function with period mathT/math, then the function mathg(x) = f(ax b)/math, where matha > 0/mat



Solve Quadratic Equation With Step By Step Math Problem Solver



Solved Q1 A Consider The Nonhomogeneous Equation X Chegg Com
Suppose that $a,b,c$ are odd $ax^2bxc=0$ has rational roots iff the discriminant is the square of an integer That is, there is an integer $d$ so that $d^2=b^24ac$2an1 0 ∞ ∫ xne−axdx= n!If x = 1/2 is a zero of the polynomial p(x) = 8x^3 ax^2 x 2, find the value of a asked Aug 7, 18 in Mathematics by Sonu khan ( 356k points) factorization of polynomials



Geometrical Representation Of Zeroes Of A Polynomial Videos Examples


Let For A A1 0 F X Ax 2 Bx C G X A1x 2 B1x C1 And P X F X G X If P X 0 Sarthaks Econnect Largest Online Education Community
Online math solver with free step by step solutions to algebra, calculus, and other math problems Get help on the web or with our math appCertain, in basic terms attempt this First, improve the polynomial expression so that you get Ax^2 Bx C Then, you ought to attempt to "comprehensive the sq" on your case, you've 4x^2 6x 5 What I do is divide by 4 and multiply by 4 4 ( x^2 3/2 x 5/4) Then, you've the expression contained in the parenthesisP(X>5) = P(X=6 or X=7 or X=8 ) " " = P(X=6)P(X=7)P(X=8 ) " " = 0105 " " = 08 Alternatively P(X>5) = 1P(X



Zero Of A Linear Polynomial Solved Examples Algebra Cuemath



Solved Show That If Y Ax B A 0 Then Corr X Y 1 O Chegg Com
Course Title MATH 0170;The expected value (or mean) of X, where X is a discrete random variable, is a weighted average of the possible values that X can take, each value being weighted according to the probability of that event occurring The expected value of X is usually written as E(X) or m E(X) = S x P(X = x) So the expected value is the sum of (each of the possible outcomes) × (the probability of theP ax2 bx c dx= 1 p a ln 2ax b 2 p a(ax2 bx c) (40)Z x p ax2 bx c dx= 1 a p ax2 bx c 2 b 2a3=2 ln 2ax b 2 p a(ax bx c) (41) Z dx (a2 x2)3=2 = x a 2 p a x2 Integrals with Logarithms (42) Z lnaxdx= xlnax x (43) Z xlnxdx= 1 2 x2 lnx x2 4 (44) Z x2 lnxdx= 1 3 x3 lnx x3 9 (45) Z xn lnxdx= xn1 lnx n 1 1 (n 1)2 ;



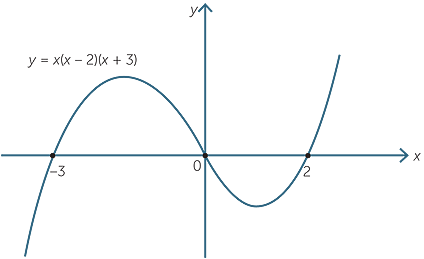
Polynomials The Degree Of Ax N If A Does Not Equal 0 The Degree Of Ax N Is N The Degree Of A Nonzero Constant Is 0 The Constant 0 Has No


Polynomials
A W x R n Ax 0 A M m n R subset R n b W x R n Ax b b 6 0 A M m n R subset R n A w x r n ax 0 a m m n r subset r n b w x r n ax b b School University of Illinois, Urbana Champaign;So that's going to be all of the x's that satisfy Ax is equal to 5, minus 5 So x1, x2 is going to be equal to b1, it's going to be equal to 5, 0 plus x2, plus any scale or multiple of the vector 3, 1 So our solution set is going to be, you take the vector 5, 0 so maybe the vector 5, 0, specifies this position right here and then you'reFind p'(x) which will be a quadratic, and solve for its routes at the maxima and minima p'(x) = 3ax^2 1 = 0 at the maxima and minima or x^2 1/(3a) = 0 there are two solution sets, one for a > 0 and one for a < 0, but for a > 0 the factors are (x 1/sqrt(3a)) (x 1/sqrt(3a))


Find The Zero Of The Polynomial P X Cx D C 0 C And D Are Real Numbers


Let A B C R If F X Ax 2 Bx C Be Such That A B C 3 And F X Y F X F Y
Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historySolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreIf x – a is indeed a factor of p(x), then the remainder after division by x – a will be zero That is p(x) = (x – a)q(x) In terms of the Remainder Theorem, this means that, if x – a is a factor of p(x), then the remainder, when we do synthetic division by x = a, will be zero



Ex 2 2 3 Verify Whether Following Are Zeroes Of The Ex 2 2



Find Zero Of Polynomial P X Ax B A Is Not Equal To 0 Brainly In
N6= 1 (46) ZP(X>5) = P(X=6 or X=7 or X=8 ) " " = P(X=6)P(X=7)P(X=8 ) " " = 0105 " " = 08 Alternatively P(X>5) = 1P(XP(X>5) = 08 The standard notation is to use a lower case letter to represent an actual event, and an upper case letter for the Random Variable used to measure the probability of the event occurring Thus the correct table would be And then;


If Ax Bx C 0 And A B C 0 What Would Be The Value S Of X Quora



Zero Of The Polynomial P X x A Is Not Equal To 0 Math Polynomials Meritnation Com
Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreLim x → a (axxa/xxaa)=1 , then (A) a=1 (B) a=0 (C) a=e (D) none of these Check Answer and Solution for above Mathematics question Tardigrade• A ≥ 0 if and only if λmin(A) ≥ 0, ie, all eigenvalues are nonnegative • not the same as A ij ≥ 0 for all i,j we say A is positive definite if x T Ax > 0 for all x 6= 0



Q11 Solve For X 1 A B X 1 A 1 B 1 X Quadratic Equations Class 10 Youtube



If A 0 Then Function F X Ax Bx C Has Minimum Value At Quora
See below note for this problem we will use the property of the sum and product of roots of a quadratic that is if " "alpha" " & " "beta are the roots of px^2qxr=0 then alphabeta=q/p alphabeta =r/p _____ x^2axb=0(1) x^2cxd=0(2) let the common root be alpha for eqn(1) alphaalpha=a =>alpha=a/2 " & "alpha^2=b for the eqn(2) let the second root be" "beta then alphabeta=cT or F if the discriminant b^2 4ac = 0, the graph of f(x) = ax^2 bx c, a=/= 0, will touch the xaxis at its vertex The graph has two distinct xintercepts if b^2 4ac greater than 0, which of the following conclusions can be made about the graph of f(x) = ax^2 bx c, a=/= 0?X p x h is a solution to Ax = b To do this, we just need to plug in x p x h for x in the equation Ax = b and show that the equation still holds Using the properties of matrix operations, A(x p x h) = Ax p Ax h = b0 = b, so x p x h is a solution to Ax = b (b) Prove that if x 1 is a solution to Ax = b, then x 1 x p is a solution to Ax



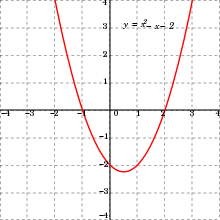
Quadratic Equation Wikipedia


If A And B Are The Roots Of The Equation X2 Ax B 0 Then The Least Value Of The Expression Is X Belongs To R Quora
Going to the answer with wrong method is absolutely wrong Thank You Have a great timeCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historyExplain (b) Suppose X ∈ P Is A Degenerate BFS Must The Product X11 ·



Sum And Product Of Zeros In Quadratic Polynomial Solved Examples Algebra Cuemath


If Ax Bx C 0 And A B C 0 What Would Be The Value S Of X Quora
Uploaded By curie4873 Pages 2 This preview shows page 2 out of 2 pages(v) p(x) = 3x (vi) p(x) = ax, a ≠ 0 (vii) p(x) = cx d, c ≠ 0, c, d are real numbers Find the zero of the polynomial in each of the following cases (i) p(x) = x 5 (ii) p(x) = x – 5 (iii) p(x) = 2x 5 (iv) p(x) = 3x – 2P(x) = ax^2 bx c P(0)= a(0) b(0) c = 1 => c=1 P(1) = a(1 *1) b(1) 1 = 6 => ab=5 ——— A P(1)= a(1 * 1) b(1) 1 =2 => ab = 1 ——— B



Solve For X 1 A B X 1 A 1 B 1 X With Video Teachoo



If The Zeroes Of The Quadratic Polynomial Ax 2 Bx C Where C Ne 0 Are Equal Then Youtube
Question Let P = {x ∈ R 100 Ax = B, X11, · · · , X ≥ 0, X100 = 0} Be A Polyhedron, Where A Is An M × 100 Matrix (1 ≤ M ≤ 100) With Linearly Independent Rows And Xi Are The Components Of The Vector X (a) For Which Values Of M Is It Possible That P Has A Degenerate BFS?P(X>5) = 08 The standard notation is to use a lower case letter to represent an actual event, and an upper case letter for the Random Variable used to measure the probability of the event occurring Thus the correct table would be And then;So if det (A) ≠ 0, then AX = B has exactly one solution If det (A) = 0, then AX = B has infinite solutions or no solutions


If A B Are The Roots Of The Equation Ax 2 Bx C 0 Find A Quadratic Equation With Roots A 3 And B 3 In Terms Of A B And C Quora



For The Function F X Sin 2 Ax X 2 When X 0 And F X 1 Whe
Example 9 If ax 3 bx 2 x – 6 has x 2 as a factor and leaves a remainder 4 when divided by (x – 2), find the values of a and b Solution Example 10 If both x – 2 and x – 1/2 are factors of px 2 5x r, show that p = r



Solving Cubic Equations Solutions Examples Videos



Cubic Equation Wikipedia



If The Diagram In Fig 2 22 Shows The Graph Of The Polynomial F X Ax Bx C Then A A Gt 0 Brainly In



Mcq Questions For Class 10 Maths Polynomials With Answers Version Weekly



P Of X Ax A Is Not Equal To 0 Find Zeros Of Polynomial Brainly In



Let A B C Be Real Numbers With A 0 And Let Alpha Beta Be The Roots Of The Equation Ax 2 Bx C 0 Express The Roots Of A 3x 2



Geometrical Representation Of Zeroes Of A Polynomial Videos Examples


If F X 1 Coskx Xsinx X 0 1 2 X 0 Is Continuous At X 0 Find K Sarthaks Econnect Largest Online Education Community


Washingtonlee Apsva Us Wp Content Uploads Sites 38 17 08 Differential Calculus Practice Problems Key Pdf



Statement 1 If Ad Ne 0 Then F X Ax B Cx D Cannot Att


The Graph Of The Polynomial P X X 5 Ax 4 Bx 3 Cx 2 Dx E Has Five Distinct X Intercepts One Of Which Is At 0 0 Which Coefficients Cannot Be Zero A B C



Solved Show That If Y Ax B A 0 Then Corr X Y 1 O Chegg Com


Quadratic Function Wikipedia



If Ax 2 Bx C 0 And Bx 2 Cx A 0 Have A Common Root And Abc 0 Then A 3 B 3 C 3abc



If P X Ax 2 Bx C Q X Ax 2 Dx C Where Ac 0 Then P X Q X 0 Has Youtube



Exploring The Solution Set Of Ax B Video Khan Academy



Find The Condition That Ax 2 Bx C 0 May Have I Both Roots Positive Ii Both Negative Roots Iii Roots Are Equal In Magnitude But Opposite In Sign



Sum And Product Of Zeros In Quadratic Polynomial Solved Examples Algebra Cuemath


If A B Y C Z A X B C Z A X B Y C 0 Then Using Properties Of Determinants Find The Value Of A X B Y C Z Where X Y Z 0 Sarthaks Econnect Largest Online Education Community
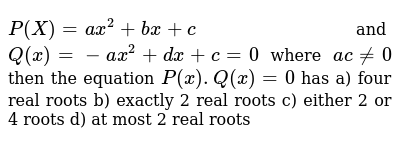


P X Ax 2 Bx C And Q X Ax 2 Dx C 0 Where Ac 0 Then The
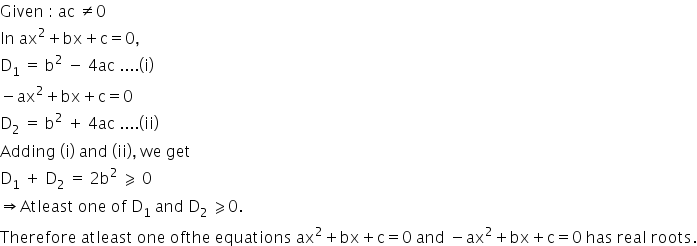


If A B C Are Real Numbers Such That Ac Not Equal To 0 Then Show That At Least One Of The Equations Ax 2 Bx C 0 And Ax 2 Bx



Linear Transformation T X Ax Xa And Determinant Of Matrix Representation Problems In Mathematics



Remainder Theorem Examples Video Khan Academy


Polynomial Wikipedia


If The Zeroes Of The Quadratic Polynomial Ax2 Bx C Where C 0 Are Equal Then Studyrankersonline



Rd Sharma Class 9 Solutions Maths Chapter 6 Factorization Of Polynomials



Find The Zero Of The Polynomial P X Cx D C Is Not Equal To 0 C D Are Real Numbers Brainly In


Http Www Daviddelgado Blogsek Es Files 16 09 Qb 14 Math Sl 3 Pdf



Find The Zero Of The Polynomial P X Ax A 0


Cbse 10 Math Ncert Solutions



Ncert Solutions For Class 9 Maths Chapter 2 Polynomials Toppers Bulletin
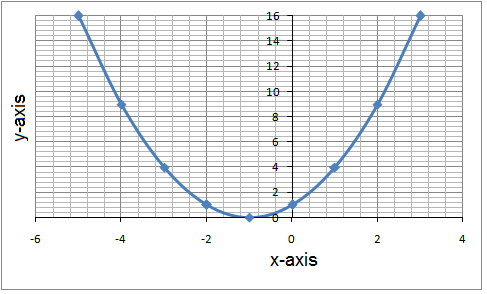


The Graph Of Y Ax 2 Bx C Algebra 1 Quadratic Equations Mathplanet



Ex 13 1 14 Evaluate Lim X 0 Sin Ax Sin Bx Class 11 Cbse



Solved An Equation In The Form 𝑦 𝑝 𝑥 𝑦 𝑞 𝑥 𝑦𝑛y P X Y Q Chegg Com


Find The Zero Of The Polynomial P X 3x 5



Condition For One Common Root X 2 Ax B 0 And X 2 Bx A 0 Youtube



Polynomials The Degree Of Ax N If A Does Not Equal 0 The Degree Of Ax N Is N The Degree Of A Nonzero Constant Is 0 The Constant 0 Has No


Search Q Zero Polynomial Example Tbm Isch
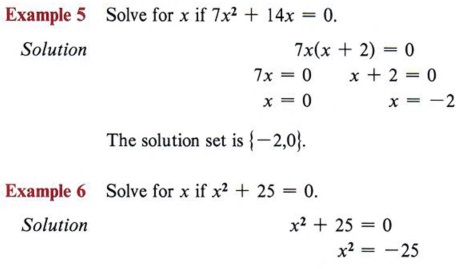


Solve Quadratic Equation With Step By Step Math Problem Solver


Let For A A1 0 F X Ax 2 Bx C G X A1x 2 B1x C1 And P X F X G X If P X 0 Sarthaks Econnect Largest Online Education Community



Chapter 1 Maths 3
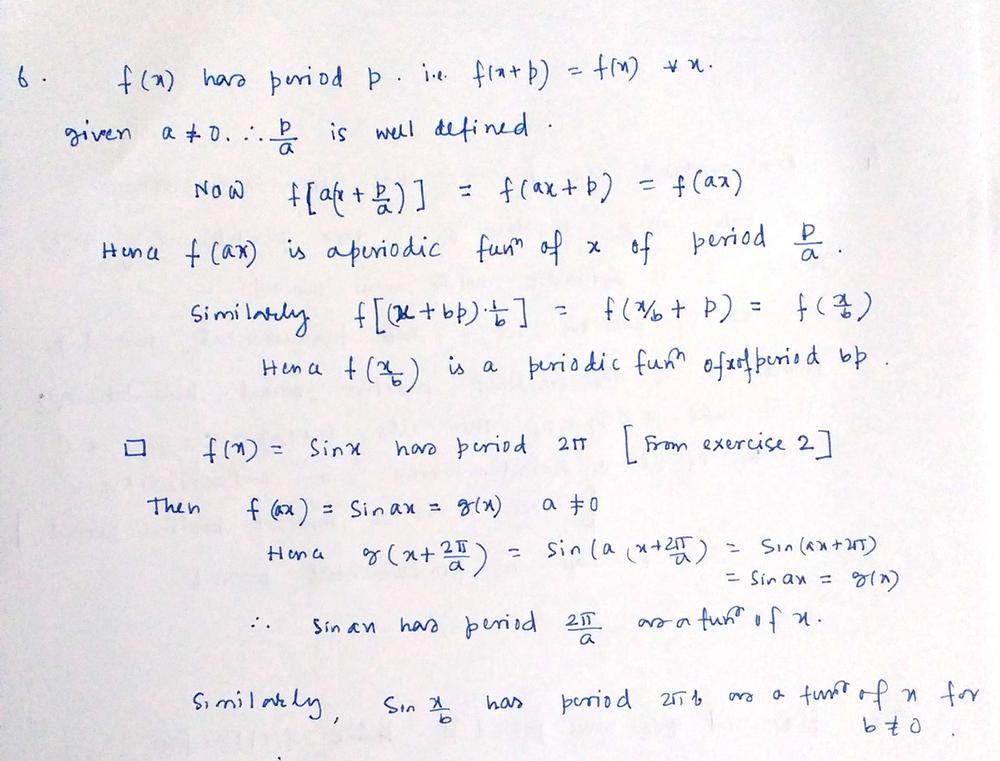


If F X Has Period P Show That F Ax A 0 And F X B B 0 Are Periodic Functions Of X Of Periods P A And Bp Respectively Give Examples Homework Help And Answers Slader


Roots Of Quadratic Equation Ax 2 Bx C At Infinity Mathematics Stack Exchange



Solved An Equation In The Form 𝑦 𝑝 𝑥 𝑦 𝑞 𝑥 𝑦𝑛y P X Y Q Chegg Com



Find Zero Of Polynomial P X Ax A Not Equal To 0



Solved An Equation In The Form 𝑦 𝑝 𝑥 𝑦 𝑞 𝑥 𝑦𝑛y P X Y Q Chegg Com



Zero Of The Polynomial P X Ax A 0 Brainly In


Http Www Daviddelgado Blogsek Es Files 16 09 Qb 14 Math Sl 3 Pdf



Find A Quadratic Polynomial Whose Zeroes Are Reciprocals Of The Zeroes Of The Polynomial Ax2 Bx C A Brainly In


Quadratic Equations Expression Zeroes Roots Formation Example Solution Algebra



Solve A X B B X A 2 Where X Is Not Equal To A B Mathematics Topperlearning Com Dur9rtcc



Chapter 1 Functions



If One Zero Of A Quadratic Polynomial P X Ax 2 Bx C Is Square Of The Other Then Give The Youtube



Ex 2 2 4 Find The Zero Of The Polynomial In Each Of Ex 2 2



Chapter 1 Maths 3



Zero Of The Polynomial P X Ax A 0 Brainly In



For The Quadratic Equation Ax 2 Bx C 0 A B C Q If D 0 Then Choose The Correct Option In Respect To The Statements Below P



Class 10 Maths Chapter 2 Ncert Exemplar Solution Part Ii



What Will The Quotient And Remainder Be On Division Of Ax2 Bx C By Px3 Qx2 Rx S P 0 It Brainly In



Find A Zero Of The Polynomial P X Ax B Ane0 And A B Are Real Numbers Youtube



Find The Zero Of The Polynomial In Each Of The Following Eases I



Ex 2 2 3 Verify Whether Following Are Zeroes Of The Ex 2 2



Remainder Theorem Method Examples


If The Zeroes Of A Quadratic Polynomial Ax2 Bx C Are Both Positive Then A B And C All Have The Same Sign Studyrankersonline
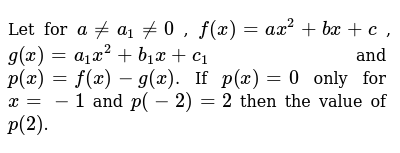


Let For A A 1 0 F X Ax 2 Bx C G X A 1x 2 B 1x C 1
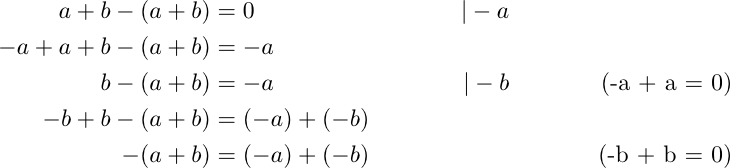


Why A 0 0 And Other Proofs Of The Obvious By Slawomir Chodnicki The Startup Medium



A Polynomial P X A O X N A 1 X N 1 A N 1 X A N
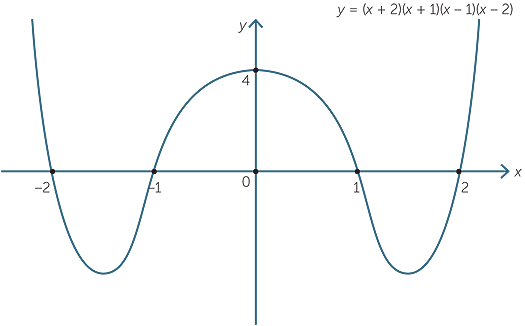


Polynomials



P X Ax A Is Not Equal To A Brainly In


Q Tbn And9gcq6gf25op9dejp5qxofv69ixpoa0t3nh9dd6spopldy2pvo9a Usqp Cau


コメント
コメントを投稿